TowerPeak 高層建築結構（含基礎）的靜力和動力時程彈塑性分析
高层建筑结构（含基础）的静力和动力时程弹塑性分析
技术研究和程序开发
作者：赖玉武
2016年9月6日
|
目录 |
页码 |
| 第一章 简介 | 1 |
| 第二章 基本理论 | 5 |
| 2.1 由截面的内力导出截面的应力和应变或由截面的应力导出截面的内力 | 5 |
| 2.2 由已知应变和弹塑性本构模型求截面的内力(P,Mx和My) | 8 |
|
|
10 |
|
|
10 |
|
2.5 由结构刚度的减少引起的迭代运算过程 |
13 |
|
|
17 |
|
|
17 |
|
|
18 |
|
|
21 |
| 3.4静力弹塑性分析的计算过程 | 24 |
|
|
29 |
|
|
33 |
第一章 简介 TowerPeak所采用的主要技术如下：
（1） TowerPeak把楼板、墙体、柱、斜撑、梁、承台、地基梁、桩作为结构构件一次性全部同时纳入计算，对它们的每个结点均作六个自由度考虑，对杆件（如柱、梁、桩等）按结构力学方法分析，对楼板、墙肢和承台板按“厚薄板”板元之有限元方法分析。
（2） 在上部结构方面，TowerPeak采用多重子结构方法，它以每层的柱、墙肢和斜撑与楼板、梁的交点（简称主结点，不是主结点的称为副结点）所组成的刚度[Ks]为单位，从顶层到底层进行刚度和荷载的静力凝聚（简称凝聚）、传递，然后从底层向顶层回代。在基础结构方面，以底层的柱、墙肢和斜撑及桩与承台板、地基梁的交点以及连系梁与承台的交点作为主结点所形成的刚度纳入整体后进行凝聚、传递和回代。对于墙肢面的刚度矩阵（[Kw]）、层间子结构的刚度矩阵（[Ke]）、
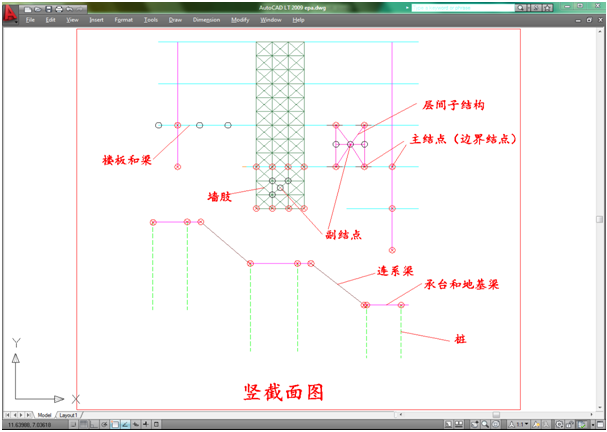
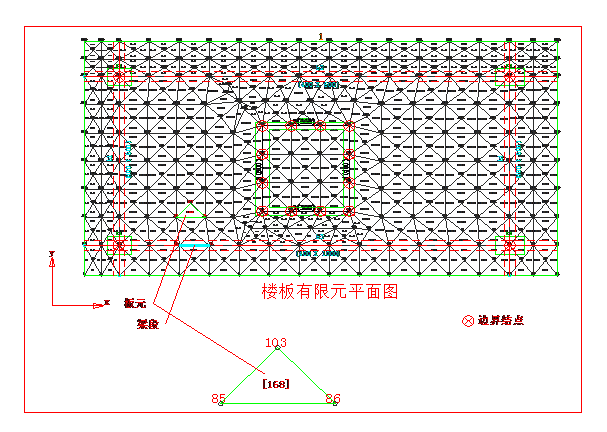
楼板与梁（按通过节点分为若干梁段）的刚度矩阵（[Kf]）、承台板和地基梁（按通过节点分为若干梁段）的刚度矩阵（[Kc]），为了把它们凝聚到主结点，必须把副结点排在前面，主结点排在后面，如下图所示：
图1-1 图1-2 （3） 在进行弹塑性分析过程中，由于构件截面进入塑性变形阶段或超过设定的应变限值而形成塑性铰或断开（这里，杆件假设为纤维模型，板元仍为板元，但组成板元的各结点的沿x和y两截面以单位宽度构成矩形截面，并包含已计算的截面配筋区域，TowerPeak也假设这两个截面为纤维模型进行应力应变计算），不断形成新的刚度矩阵 [Kn]，此时的方程为
[Kn][X]=[B]
令 [Kn]=[K0]-[Kr]， [K0]为原始未凝聚刚度矩阵
上述方程变为
[K0][Xj]=[B]+[Kr][Xi]
（这里：j=i+1）
对上式进行迭代，便可得对应于[Kn]的位移，当[Kr]<0.5*[K0]（这个表达式不太准确，它的意思是结构的整体刚度折减不超过或等于原始刚度的一半，以迭代能否收敛为依据）时，迭代基本上收敛，[Kr]越小，收敛越快，如果不收敛，则认为整体结构已经破坏，这也是TowerPeak的假设之一，详细描述见下一章。
（4） 对于静力弹塑性分析，在进行结构振动分析时(TowerPeak采用子空间迭代法)，每一步子空间迭代需要由
[Ki][V]=[M][V]
求解各振型的位移矢量[Vj]，[Ki]是由于构件截面进入塑性变形阶段或超过
设定的应变限值而形成塑性铰或断开，形成的新刚度矩阵。
将上式改写成：
([K0]-[Kr])[V]=[M][V] 或
[K0][Vj]=[M][Vi]+[Kr][Vi] （这里：j=i+1）
则可采用上一段的方法进行迭代。
（5） TowerPeak 也可考虑截面的各材料的刚度退化（在EPA档案里定义），如果某材料需要考虑刚度退化，则在某一轮的应变计算中，其截面形心处的应变必须加进△ε，而△ε为上一轮的相应应变与屈服应变之差，如果这个差值与截面形心处的应变的正负号相反，则△ε=0。在相同的轴力下，应变越大，轴向刚度越小，与刚度退化的含义相同。
（6） 在完成结构的常规计算后，弹塑性分析EPA作为后处理程序，需要准备的数据极少，加上这些数据可以自动产生，几乎马上可以进行弹塑性分析。
在上述的第(3)、(4)段中，均不需要刚度矩阵的分解，只需要进行 计算结果显示各次加载（静力弹塑性分析）或各时刻（动力弹塑性分析）的各构件（墙、柱、楼板、梁、承台板、地基梁和桩）在何处变为塑性铰或何种破坏类型（分别为拉弯、压弯和剪切破坏）而断开，各层的位移和层间位移角，并把结果显示在立体图上。
需要强调的是，如果上部结构不与基础作为整体一起而单独进行分析的话，所得结果与按实际情况作为整体分析的差别往往很大，所以对于前者，理论和分析再怎么精确，也无补于事，而TowerPeak已基本上弥补了这个致命缺陷。
第二章
基本理论
2.1 由截面的内力导出截面的应力和应变或由截面的应力导出截面的内力
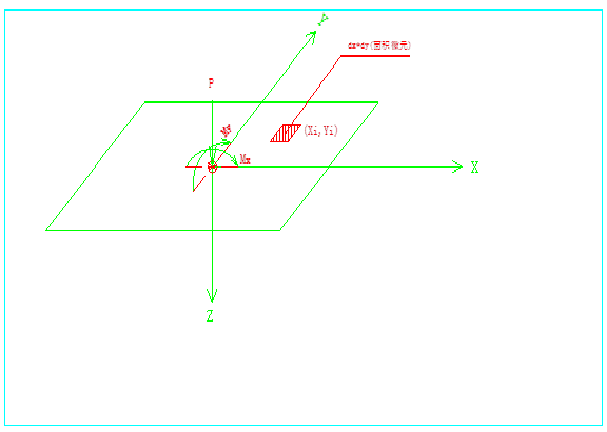
设有一平面，如图2-1-1，未受力时位于z=0，当施加一位于坐标原点的点荷载P，Mx，
图 2-1-1
My，根据材料力学的平面变形假设，变形后的平面仍为平面， 假设它的应变平面方程为
作用于平面上某一点的应力正比于z（根据弹性假设）
其中β是比例常数。根据力的平衡条件可得
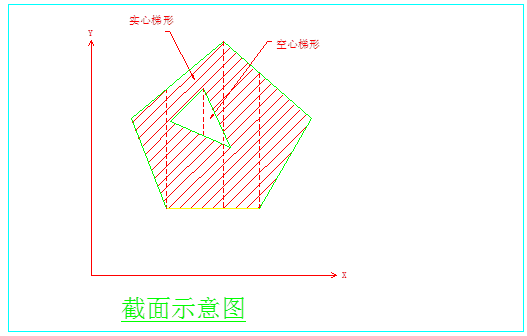
这里假设截面为单一材料，对多种材料构成的组合截面，上述方程的左边则为各材料区域的积分总和。 对于任一形状的平面图形，如图2-1-2，总可以把它精确地或近似地分成有限个如下图所示的梯形（包括三角形），这些梯形有实有空，先对这些梯形逐个积分，然后迭加（实的梯形积分值为正，空的为负）就可以求出整个平面的解。
展开2-1-3式得：
设该平面划分为n个梯形，则上式最后化为
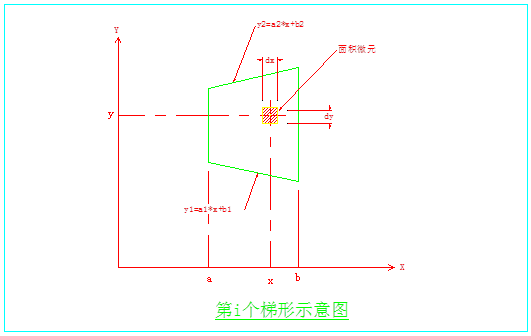
其中 fi=1对应于实的梯形，fi=-1对应的空的梯形。各梯形的分项积分如下：
如果已知P，Mx，My，则从2-1-5式可解得a，b，c，代入2-1-2式可得平面上任一点的正应力б。由a，b，c可得a´，b´，c´，再由2-1-1式可得平面上任一点的应变Z 。
反之，如果已知平面上的正应力分布（即知a，b，c），则直接从2-1-2式得出P，Mx，My。 2.2由已知应变和弹塑性本构模型求截面的内力(P,Mx和My)
假定截面在变形后仍为平面，故截面的应变由下式表示： ε=a x+b y+c (平面方程)
如下图所示， 线段1或2的应力
P= ∫h dA
Mx= ∫f x dA (沿截面x方向的弯矩)
My= ∫g y dA (沿截面y方向的弯矩) 对任意截面形状，上述各式可用2.1节的方法求出。 当对各种材料（对应于截面上的不同区域）的本构模型上的所有线段（注意，当某些线段没有对应到截面上的区域，此时的P、Mx和My均为零）对应的P、Mx和My进行累加，即可得全截面在上述应变下的总内力
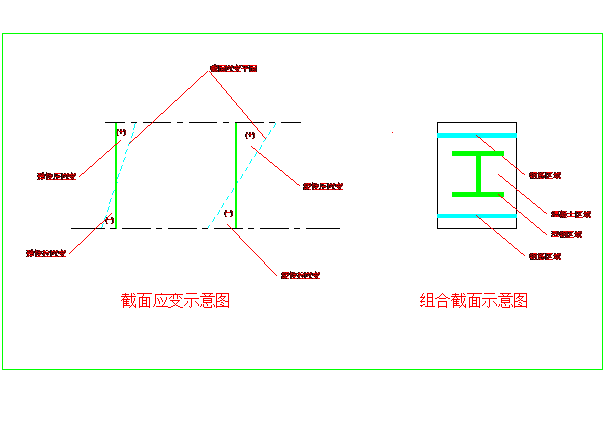
Nt、Mxt和Myt 注意：用现有的PC，一秒钟可完成3万个截面的应变或累积内力运算,所以该运算占用的时间很少。 2.3 实际弹塑性应变的推导 在弹塑性分析的每一轮结构计算中，各构件采用各自的弹性模量（定义于BCD档案），其计算内力为P、Mx和My，按上一节所述，其对应的应变方程（如下图）为
ε=a x+b y+c
(2-3-1)
第三章 图3-1
（2-1-1）
（2-1-2）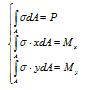
（2-1-3）
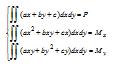（2-1-4）
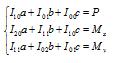（2-1-5）
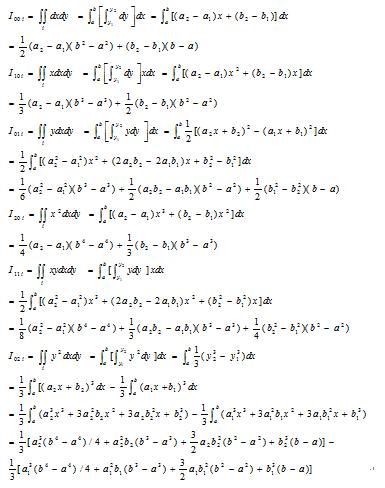
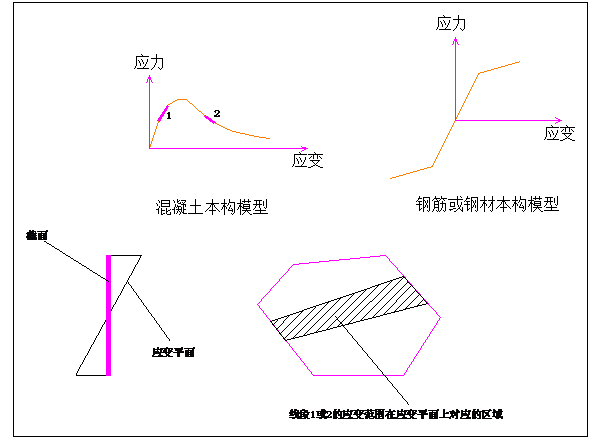
σ=d ε+e （对于线段1，d>0，对于线段2，d<0 ）
=d(a x+b y+c)+e
=f x+g y+h
可知应力平面也为一平面方程。
现对线段1或2的应变范围在应变平面上对应区域的应力进行积分，可得
由此应变和材料的本构模型（定义于EPA档案），按 2.2 节求截面的弹塑性反力P´、Mx´和My´，再由它们求相应的应变（假设为平面），其应变方程为
ε´=a´ x+b´ y+c´ （2-3-2）
由于由P´，Mx´和My´产生的应变效果一般小于内力P，Mx和My所产生的，为接近或等于P、Mx和My，实际的应变（称为“实际弹塑性应变”）为
ε＂ =a＂ x+b＂ y+c＂
(2-3-3)
这里，a＂=a ka; b＂=b kb; c＂=c kc
(ka、kb、kc不应小于1.0)
如采用 [应变分量]方法（定义于EPA档案）来确定弹塑性应变与弹性应变的比例，则
ka=a / a´; kb=b/ b´; kc=c/ c´
（2-3-4）
如采用 [应变体积]方法（定义于EPA档案）来确定弹塑性应变与弹性应变的比例，则
ka=kb=kc=k
这里，k 为 ε的应变体积除以 ε´的应变体积。
应变体积为正应变对相应的区域积分和负应变对相应的区域积分的绝对值之和。
如果按实际弹塑性应变调低构件截面的刚度（定义于EPA档案），则构件截面的折减后
面积： A=A0 kc
沿截面x方向的截面惯性矩： Iyy=Iyy0 ka
沿截面y方向的截面惯性矩： Ixx=Ixx0 kb
其中：A0、Iyy0和Ixx0为整个截面的原有面积和惯性矩。
并将它们使用于下一轮计算中。
2.4 动力响应振动分析
动力响应振动分析就是求系统运动方程
[M][A]+[C][S]+[K][D]=[F]+[P]
满足初始条件 [S]=[S0]，[D]=[D0]的解，
这里：
[M]---结构的质量矩阵
[K]---结构的刚度矩阵
[C]---结构的阻尼矩阵，采用瑞利阻尼，即 [C]=α[M]+β[K]，
瑞利阻尼常数由结
构的第1和第2自振频率和相应的两个阻尼比确定：
α=2ω1ω2（ξ1ω2-ξ2ω1）/（ω2ω2-ω1ω1）
β=2（ξ2ω2-ξ1ω1）/（ω2ω2-ω1ω1）
式中 ω1、ω2 分别为结构的第1和第2固有频率，ξ1、ξ2 为相应于
第1
和第2振型的阻尼比。
[F]---时刻t的动荷载矩阵，如果为地震加速度反应谱引起，则 [F]=-[M]*Ag
（这里：Ag 为地面运动加速度）。
[P]---长期荷载（或称常荷载，其组合系数定义于BCD档案）
[A]---时刻t的加速度矩阵
[S]---时刻t的速度矩阵
[D]---时刻t的位移矩阵
上述矩阵由下列结点（称为主结点）构成：
上部结构部分：由柱、墙、斜撑和层间子结构与上下楼盖（楼板和梁）的交点作为结点。
基础结构部分：由底层的柱、墙、斜撑和层间子结构与基础承台板和地基梁的交点、
各独立基础与其间的连系梁交点以及桩与基础承台板和地基梁的的交
点作为结点。
不属于上述结点的为副结点，所有副结点的刚度和质量将静力凝聚到主结点。
TowerPeak采用直接积分法中的 Wilson-θ 方法解系统运动方程，其简单计算步骤如下：
（1） 形成刚度矩阵[K]、质量矩阵[M]和阻尼矩阵[C]。
（2） 确定初始值（均设为零）。
（3） 选取时间步长Δt（定义于EPA档案），计算积分常数（取θ=1.4）：
α0=6/(θΔt)2, α1=3/(θΔt), α2=2 α1, α3= θΔt/2,
α4=α0/θ, α5=-α2/θ, α6=1-3/θ, α7=Δt/2, α8=Δt2/6
（4） 对每一时间步长Δt，形成有效刚度矩阵，
[K´]=[K]+ α0 [M]+ α1 [C]=[K]+ α0 [M]+ α1 (α[M]+β[K])
=(1+ α1β) [K]+(α0+α1α) [M]
（5） 对每一[K´]按附录A方法进行分解
（6） 计算时刻t´= t+ θΔt（前一时刻为t，以下同）的有效荷载：
[F´] t´ =[F] t´+[M]( α0[D]t+ α2 [S] t +2[A] t)+[C]( α1 [D] t +2[S] t + α3 [A] t)
并加上[P]和由于t时刻侧移产生的附加弯矩 Mxx=Pv*dy，Myy=Pv*dx (即考虑P-△效应)，这里Pv是长期荷载的竖向分量，dx、dy是节点t时刻沿x、y方向的线位移。
（7） 求解时刻t´= t+ θΔt的位移 [D] t´
（8） 计算t+ Δt时刻的加速度、速度和位移：
[A´]=α4([D´]-[D])+ α5[S]+ α6[A]
[S´]=[S]+ α7([A´]+[A])
[D´]=[D]+ △t [S]+ α8([A´]+2[A])
这里：[A´]、[S´]和[D´]分别是t+ Δt时刻的加速度、速度和位移，
[A]、[S]和[D]分别是t时刻的加速度、速度和位移。
2.5 由结构刚度的减少引起的迭代运算过程
把一般的建筑结构分为楼板、梁、柱（包括斜撑），墙、 层间子结构（杆件体系）、承台板、地基梁，承台间的连系梁和桩，见图1-1和图1-2，各子结构对应的原始刚度矩阵记为：
楼板+梁： [Kf]
层间子结构：[Ke]
墙：[Kw]
承台板+地基梁：[Kc]
上述刚度的结点排列为副结点在前，主结点在后，把它们的副结点凝聚掉之后的刚度矩阵和算符
楼板+梁： [Kf´],
层间子结构：[Ke´],
墙：[Kw],
承台板+地基梁：[Kc´],
[Ks´] 和
各子结构的原始矩阵方程(方程右边为荷载矩阵)：
[Kw][Xw]=[Bw]
[Ke][Xe]=[Be]
[Kf][Xf]=[Bf]……………………………………………………… （2-5-1）
[Kc][Xc]=[Bc]
[Ks][Xs]=[Bs]
各子结构凝聚后的矩阵方程(方程右边为荷载矩阵)：
[Kw´][Xw]=[Bw´]， [Bw´]=<Rw>
[Ke´][Xe]=[Be´]， [Be´]=<Re>
[Kf´][Xf]=[Bf´]， [Bf´]=
[Kc´][Xc]=[Bc´]， [Bc´]=
[Ks´][Xs]=[Bs´]， [Bs´]=<Rs>
对于任意一轮计算，各子结构的新刚度矩阵分别为：
[Kwi]=[Kw]-[Kwr]、
[Kei]=[Ke]-[Ker]、
[Kfi]=[Kf]-[Kfr]、
[Kci]=[Kc]-[Kcr]、
[Ksi]=[Ks]-[Ksr]
2-5-1式变成（注意，下式的[B]和[X]可能和2-5-1式不同）：
[Kwi][Xw]=[Bw]
[Kei][Xe]=[Be]
[Kfi][Xf]=[Bf]……………………………………………………… （2-5-3）
[Kci][Xc]=[Bc]
[Ksi][Xs]=[Bs]
或写成：
[Kw][Xw]=[Kwr][Xw]+[Bw]
[Ke][Xe]=[Ker] [Xe]+ [Be]
[Kf][Xf]=[Kfr] [Xf]+ [Bf]………………………………………………（2-5-4）
[Kc][Xc]=[Kcr] [Xc]+ [Bc]
[Ks][Xs]=[Ksr] [Xs]+ [Bs]
凝聚后：
[Kw´][Xw]=
[Ke´][Xe]=
[Kf´][Xf]=
[Kc´][Xc]=
[Ks´][Xs]=
这里：
上式即为TowerPeak采用的迭代方程式，迭代过程中不需要分解矩阵，而只作
对于动力弹塑性分析，上式的[Ks]为有效刚度矩阵，[Bs]为有效荷载矩阵（见上一节）, 其它全为实际刚度矩阵和荷载矩阵，但此时
对于属于板元的构件，如楼板、墙肢和承台板，则对任意一个板元，如图1-2，围绕它有n个结点，每个结点有沿x和y作为法线的两个截面，如果设定按实际弹塑性应变调低构件截面的刚度，则由此2n个截面的kc（见式2-3-4）平均值作为面内刚度的折减系数，再由2n个截面的kb（见式2-3-4）平均值作为面外（弯曲）刚度的折减系数，并将折减后的刚度加入各相应子结构的刚度矩阵，否则用原始的该板元刚度。如2n个截面中的其中一个的截面应变达到设定的变为塑性铰的限值，则取消该板元的面外刚度，如2n个截面中的其中一个的截面应变达到设定的变为断开的限值，则取消该板元的作用。
计算和操作流程
3.1 设定BCD档案如下
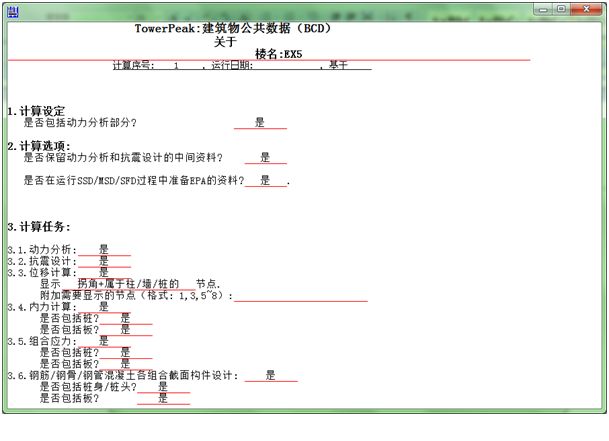
3.2 运行SSD、MSD或SFD档案，如下所示：
图3-2-1 
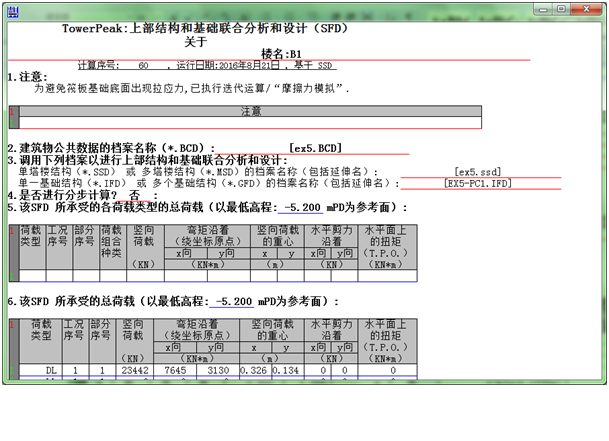
运行完成后，可得自振周期、用于静力弹塑性分析的地震底部剪力和基本水平荷载以及各构件的截面配筋，分别如下4图所示：
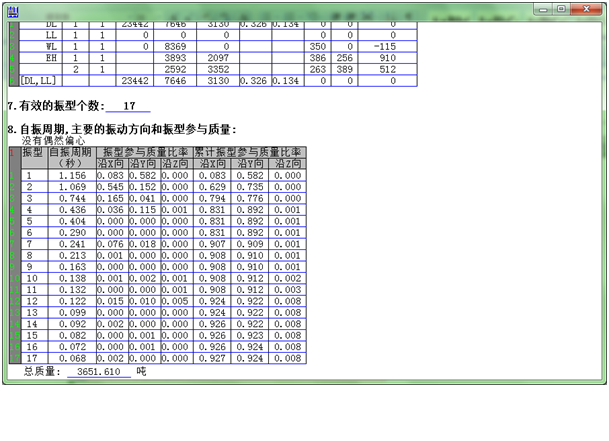
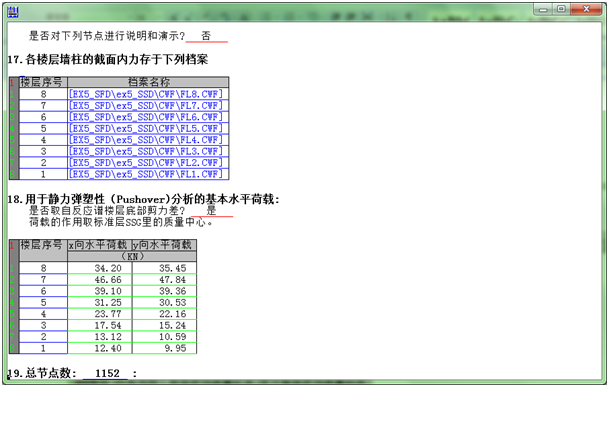
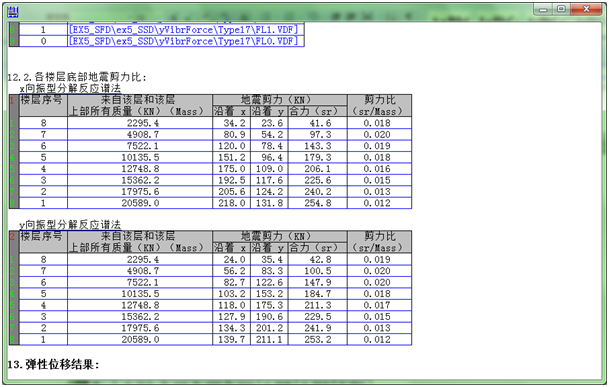
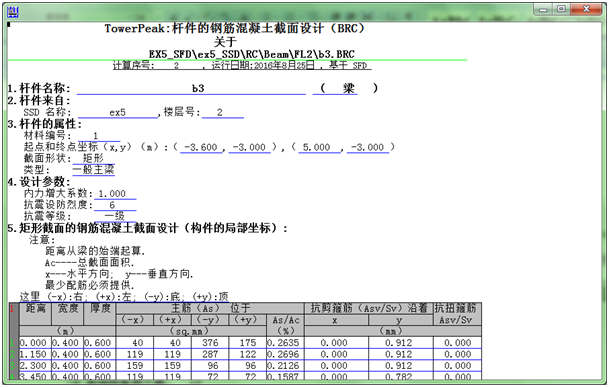
3.3 开启一个EPA档案并填写有关数据如下，
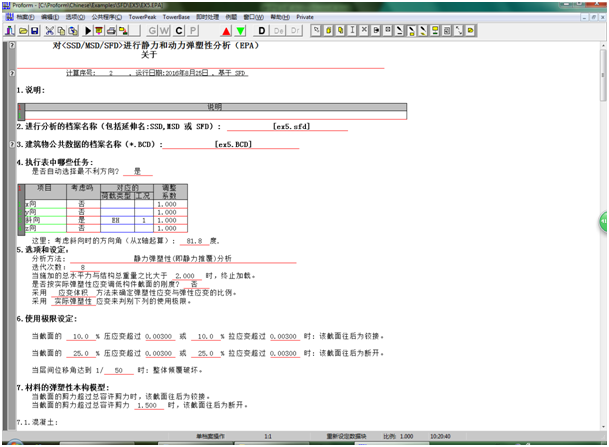
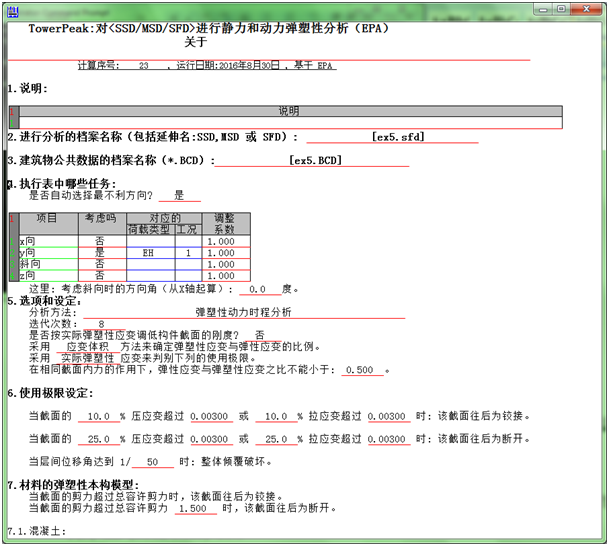
在此档案中，如果由程序自动选择最不利方向，则其方向角等于结构第一自振周期的方向，本例为 tan-1(0.582/0.083)=81.8o
执行菜单“即时处理”的[36]号命令，即可得结果如下：
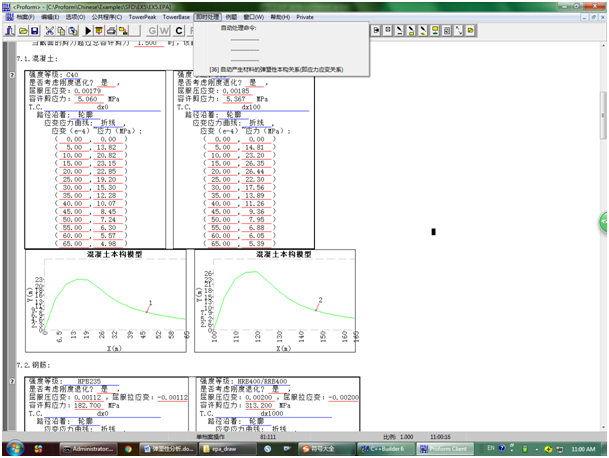
自动产生的应力应变关系来自《混凝土规范GB50010-2010》，混凝土的容许剪应力为0.8*sqr(fcu) (fcu—混凝土的标号)，钢筋和型钢的容许剪应力为0.87*fy。
3.4静力弹塑性分析的计算过程
1. TowerPeak利用图3-2-5用于静力弹塑性（Pushover)分析的基本水平荷载，自动把它们分配到节点。在第一轮计算后，TowerPeak根据应变的大小确定初始的基本水平荷载。
2. 利用已计算的钢筋量确定钢筋在所属截面的分布区域，钢筋的最小配筋率在EPA里定义如下：
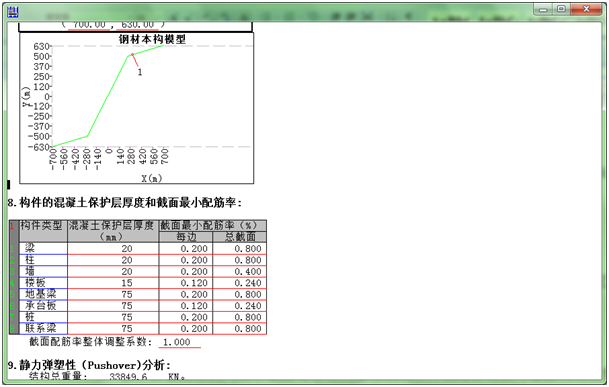
3. 按输入的加载步长，确定下一轮的水平荷载。
4. 按计算截面应变判别该截面是否达到塑性铰或断开或是否需要对截面的刚度折减，计算截面的新刚度[Kne]，与原始的刚度[Ke]比较，得出[Kre]=[Ke]-[Kne]。
5. 对各子结构的 [Kri][Xi]进行凝聚：
同时加上[P]和由于t时刻侧移产生的附加弯矩 Mxx=Pv*dy，Myy=Pv*dx (即考虑P-△效应)，这里Pv是长期荷载的竖向分量，dx、dy是节点t时刻沿x、y方向的线位移。
6. 回代各层 [Ks][Xi]=
7. 计算各构件的截面内力和截面应变。
8. 每隔 [n](在EPA里设定)次加载计算一次结构振动周期。
9. 将每次的结果存于下表：
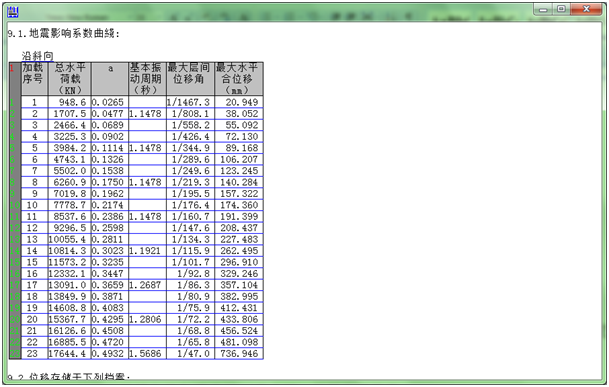
10. 判断结构是否已经整体倾覆破坏，如果未破坏，回到第4步开始新一轮计算。
11. 绘出各罕遇地震烈度和静力推覆的地震影响系数曲线并确定结构抵抗地震烈度能力:
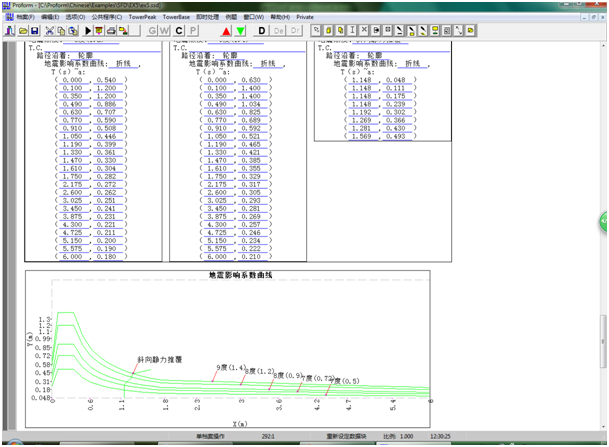
上图静力推覆的地震影响系数曲线穿过9度（1.4），表示结构能抵抗地震烈度超过9度（1.4），
余者类推。
12. 显示构件破坏情况如下：
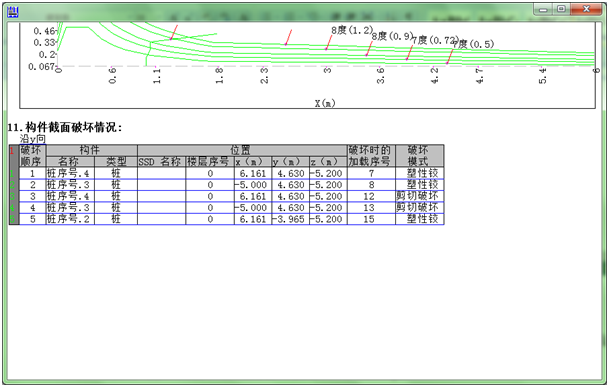
13. 绘制立体图（按“DXF”键导出到AutoCAD上）如下：
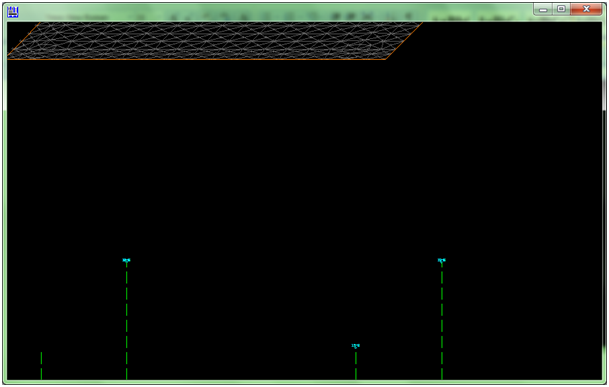
这里：节点旁边的标示7-H表示此节点在第7次加载后形成塑性铰（H），其它符号表示如下：
S---剪切破坏
C---压弯破坏
T---拉弯破坏
3.5弹塑性动力时程分析过程
1. 创建“地面运动加速度反应谱”档案ARS，如下所示：
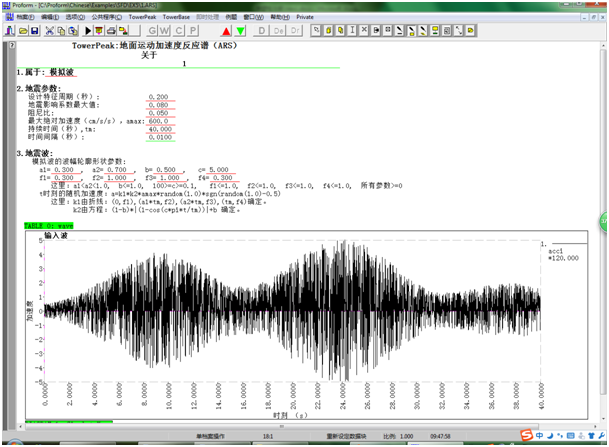
2. 与3.4节第2步相同。
3. 选取上下层连结处的结点（柱顶及墙肢与楼板或梁的交点,由程序自动选取）作为空间质点（对于不属于质点的其它结点，其刚度、质量、转动惯量和长期荷载利用静力凝聚方法凝聚到这些质点中去），对每一标准层和基础层形成各自的刚度矩阵[K]、质量矩阵[M]和阻尼矩阵[C] ，这里，
[C]= α[M]+β[K]
其中α、β是瑞利阻尼常数，由结构的第一、二振型自振频率确定：
α=2ω1ω2（ξ1ω2-ξ2ω1）/（ω2ω2-ω1ω1）
β=2（ξ2ω2-ξ1ω1）/（ω2ω2-ω1ω1）
式中 ω1、ω2 分别为结构的第1和第2固有频率，ξ1、ξ2 为相应于第1和第2振型的阻尼比。
长期荷载的荷载组合定用于BCD档案，如下所示：
4. 采用Wilson- θ法（直接积分法的一种）进行动力响应振动分析，取θ=1.4。
5. 确定初始位移[D]、速度[S]和加速度[A]，全部为零。
6. 对每一时间步长Δt，计算积分常数：
α0=6/(θΔt)2, α1=3/(θΔt), α2=2 α1, α3= θΔt/2,
α4=α0/θ, α5=-α2/θ, α6=1-3/θ, α7=Δt/2, α8=Δt2/6
7. 对每一时间步长Δt，形成有效刚度矩阵，
[K´]=[K]+α0 [M]+α1 [C]=[K]+α0 [M]+α1 (α[M]+β[K])
=(1+α1β) [K]+(α0+α1α)[M]
8. 对每一[K´]进行分解。
9. 计算时刻t´= t+θΔt（前一时刻为t，以下同）的有效荷载：
[F´]t’ =[F]t’+[M](α0[D]t+α2 [S] t +2[A] t)+[C]( α1 [D] t +2[S] t + α3 [A] t)
这里，[F]t’包括t´时刻的加速度所产生的惯性力和第2 点所述的基本静力荷载。
10. 求解时刻t´= t+θΔt的位移 [D] t’（按3.4节的第4步到第7步进行迭代，但此时的各[Kr]必须乘以 1+ α1β）
11. 计算t+Δt时刻的加速度、速度和位移：
[A´]=α4([D´]-[D])+ α5[S]+ α6[A]
[S´]=[S]+ α7([A´]+[A])
[D´]=[D]+ △t [S]+ α8([A´]+2[A])
这里：[A´]、[S´]和[D´]分别是t+Δt时刻的加速度、速度和位移，
[A]、[S]和[D]分别是t时刻的加速度、速度和位移。
12. 判断结构是否已经整体倾覆破坏，如果未破坏，回到第9步进行计算。
13. 按3.4节的第10步到第13步。
附录A 线性方程组与静力凝聚的分解方法
如下图：
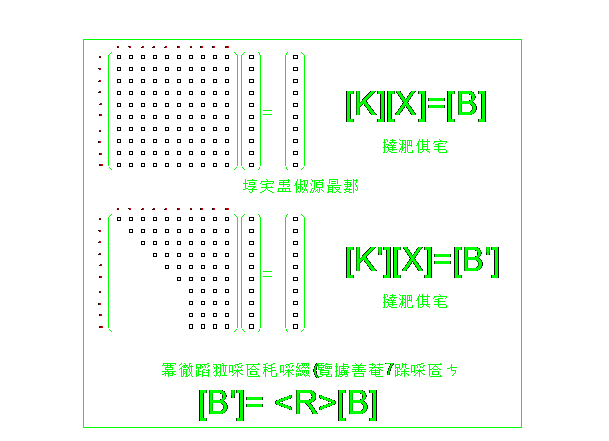
对于一个n阶原始线性方程组，当消元到第m行时，即静力凝聚（简称凝聚）掉m-1个元素（当m=n时，即为线性方程组的全解），在凝聚过程中，系数矩阵的分解(消元)非常费时，如果对每一个新的荷载矩阵，都需要对它分解一次，将无实用价值，特别是结构的刚度每时每刻都在变化，在现有的个人电脑和有限的时间内完成计算，几乎不可能，所以，本文将推导出一个算符
[B´]=
首先，把
Ni, Fij, Pij (i=1,2,…n; j=1,2,…m)
下文省略，用户或读者有兴趣，请留意以后发布。
如读者需要使用此程序，请从www.towerpeak.cn 或 www.towerpeak.hk 上免费下载和安装TowerPeak软件（包括弹塑性分析程序：EPA），并于“精选实例”EPA方面入手。